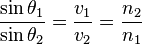|
so sleep alone tonight
My name is ღ||汇嘉||SOPHIAღ. Give me presents! On 22061996 :D [Cancer] [CHRISTIAN] PLMGSS 2.1 I love Aaron (: |
|
|
about this blog
This blog was opened by (SOPHIAARON) to accomodate (SOPHIA)'s Science journal.Do enjoy your stay here, and don't take what's not yours! tagboard
ShoutMix chat widget br> affiliates
DORCAS!!!(: MELISSA LISA LISHAN RACHEL RADIENT JANELLE JASLEY SEOWHWEE STELLA STACEY SARAH SHIYU JOYI Bue. Bue. Bue. archives
Videos. (:
-------------Physics------------Liquifaction. How to get out of a quicksand. Math Definitions : What Is Terminal Velocity. Newton's 3 laws of motion. Titration Technique using a burette How to use a pipette. Indroduction to Frictional force. Tacoma Bridge Collapsed! ---------------Chemistry---------- Forensic Video Periodic table song(: Crystal structures: graphite and diamond Chromotography- Separation of MIxtures Separation: Iron from Salt & Sand Mixture Steam Distillation Fractional Distillation Video Video Video Video Video Video Video Video Video Video Video Video Video credits
Design: doughnutcrazyIcon: morphine_kissed Do credit accordingly if you changed the icon. |
Physics 06
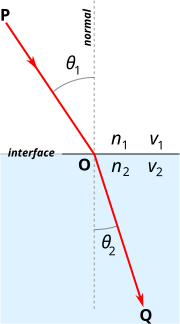
Today during lesson, Mr Lim flashed a slide on the Snell's law.I didn't quite get the formulae on the screen. Here are some of the description on Snell's law: In optics and physics, Snell's law (also known as Descartes' law, the Snell–Descartes law, and the law of refraction), is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass. The law says that the ratio of the sines of the angles of incidence and of refraction is a constant that depends on the media.
In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics and gemology to find the refractive index of a material. Snell's law is also satisfied in the metamaterials which allow light to be bent "backward" at a negative index, with a negative angle of refraction. Named after Dutch mathematician Willebrord Snellius, one of its discoverers, Snell's law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of velocities in the two media, or equivalent to the opposite ratio of the indices of refraction: or Snell's law follows from Fermat's principle of least time, which in turn follows from the propagation of light as waves.
Above are taken from http://en.wikipedia.org/wiki/Snell's_law
Summary:
Snell's law gives the relationship between angles of incidence and refraction for a wave impinging on an interface between two media with different indices of refraction. The law follows from the boundary condition that a wave be continuous across a boundary, which requires that the phase of the wave be constant on any given plane, resulting in |